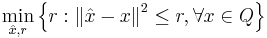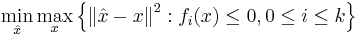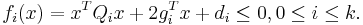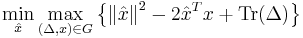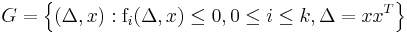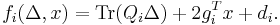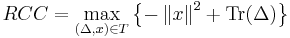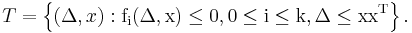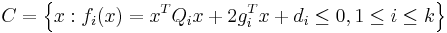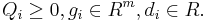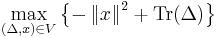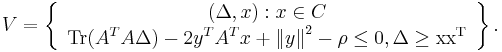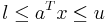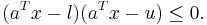Chebyshev center

In geometry, the Chebyshev center of a bounded set Q having non-empty interior is the center of the minimal-radius ball enclosing the entire set Q, or, alternatively, the center of largest inscribed ball of Q[1] .

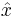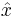In the field of parameter estimation, the Chebyshev center approach tries to find an estimator \hat x for x given the feasibility set Q , such that \hat x minimizes the worst possible estimation error for x (e.g. best worst case).

Contents

Mathematical representation

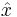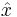There exist several alternative representations for the Chebyshev center. Consider the set Q and denote its Chebyshev center by \hat{x}. \hat{x} can be computed by solving:

\min_{{\hat x},r} \left\{ r:\left\| {\hat x} - x \right\|^2 \leq r, \forall x \in Q \right\}

or alternatively by solving:

Failed to parse (PNG conversion failed;

check for correct installation of latex, dvips, gs, and convert): \operatorname*{\arg\min}_{\hat{x}} \max_{x \in Q} \left\| x - \hat x \right\|^2. [2]

Some important optimization properties of the Chebyshev Center are:

Despite these properties, finding the Chebyshev center may be a hard numerical optimization problem. For example, in the second representation above, the inner maximization is non-convex if the set Q is not convex.

Relaxed Chebyshev center

Let us consider the case in which the set Q can be represented as the intersection of k ellipsoids.

\min_{\hat x} \max_x \left\{ \left\| {\hat x} - x \right\|^2�:f_i (x) \le 0,0 \le i \le k \right\}

with

f_i (x) = x^T Q_i x %2B 2g_i^T x %2B d_i \le 0,0 \le i \le k. \,

By introducing an additional matrix variable 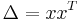\Delta = x x^T , we can write the inner maximization problem of the Chebyshev center as:

\min_{\hat x} \max_{(\Delta ,x) \in G} \left\{ \left\| {\hat x} \right\|^2 - 2{\hat x}^T x %2B \operatorname{Tr}(\Delta ) \right\}

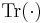where \operatorname{Tr}(\cdot) is the trace operator and

G = \left\{(\Delta ,x):{\rm{f}}_i (\Delta ,x) \le 0,0 \le i \le k,\Delta = xx^T \right\}
f_i (\Delta ,x) = \operatorname{Tr}(Q_i \Delta ) %2B 2g_i^T x %2B d_i.

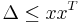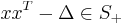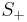Relaxing our demand on \Delta by demanding \Delta \leq xx^T , i.e. xx^T - \Delta \in S_%2B where S_%2B is the set of positive semi-definite matrices, and changing the order of the min max to max min (see the references for more details), the optimization problem can be formulated as:

RCC = \max_{(\Delta ,x) \in {T}} \left\{ - \left\| x \right\|^2 %2B \operatorname{Tr}(\Delta ) \right\}

with

{T} = \left\{ (\Delta ,x):\rm{f}_i (\Delta ,x) \le 0,0 \le i \le k,\Delta \le xx^T \right\}.

This last convex optimization problem is known as the relaxed Chebyshev center (RCC). The RCC has the following important properties:

Constrained least squares

With a few simple mathematical tricks, it can be shown that the well-known constrained least squares (CLS) problem is a relaxed version of the Chebyshev center.

The original CLS problem can be formulated as:

Failed to parse (PNG conversion failed;

check for correct installation of latex, dvips, gs, and convert): {\hat x}_{CLS} = \operatorname*{\arg\min}_{x \in C} \left\| y - Ax \right\|^2

with

{ C} = \left\{ x:f_i (x) = x^T Q_i x %2B 2g_i^T x %2B d_i \le 0,1 \le i \le k \right\}
Q_i \ge 0,g_i \in R^m ,d_i \in R.

It can be shown that this problem is equivalent to the following optimization problem:

\max_{(\Delta ,{{x}}) \in {V}} \left\{ { - \left\| {{x}} \right\|^2 %2B \operatorname{Tr}(\Delta )} \right\}

with

V = \left\{ \begin{array}{c} (\Delta ,x):x \in C{\rm{ }} \\ \operatorname{Tr}(A^T A\Delta ) - 2y^T A^T x %2B \left\| y \right\|^2 - \rho \le 0,\rm{ }\Delta \ge xx^T \\ \end{array} \right\}.

One can see that this problem is a relaxation of the Chebyshev center (though different than the RCC described above).

RCC vs. CLS

A solution set 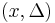(x,\Delta) for the RCC is also a solution for the CLS, and thus 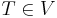T \in V . This means that the CLS estimate is the solution of a looser relaxation than that of the RCC. Hence the CLS is an upper bound for the RCC, which is an upper bound for the real Chebyshev center.

Modeling constraints

Since both the RCC and CLS are based upon relaxation of the real feasibility set Q, the form in which Q is defined affects its relaxed versions. This of course affects the quality of the RCC and CLS estimators. As a simple example consider the linear box constraints:

l \leq a^T x \leq u

which can alternatively be written as

(a^T x - l)(a^T x - u) \leq 0.

It turns out that the first representation results with an upper bound estimator for the second one, hence using it may dramatically decrease the quality of the calculated estimator.

This simple example shows us that great care should be given to the formulation of constraints when relaxation of the feasibility region is used.

See also

References

  1. ^ Boyd, Stephen P.; Vandenberghe, Lieven (2004). Convex optimization. New York: Cambridge. ISBN 9780521833783. 
  2. ^ Boyd, Stephen P.; Vandenberghe, Lieven (2004) (pdf). Convex Optimization. Cambridge University Press. ISBN 9780521833783. http://www.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf. Retrieved October 15, 2011.